В этой публикации мы представим очень простую модель солнечного элемента. Многие понятия, представленные в этой главе, будут новыми, но, тем не менее, основные принципы работы солнечной батареи должны быть понятны. Все аспекты, представленные здесь, будут более подробно рассмотрены далее.
Принцип работы солнечных батарей основан на фотовольтаическом эффекте, т.е. возникновении разности потенциалов на стыке двух различных материалов в ответ на электромагнитное излучение. Фотовольтаический эффект тесно связан с фотоэлектрическим эффектом, когда электроны испускаются из материала, поглотившего свет с частотой выше пороговой частоты, зависящей от материала. В 1905 году Альберт Эйнштейн понял, что этот эффект можно объяснить, если предположить, что свет состоит из четко определенных квантов энергии, называемых фотонами. Энергия такого фотона определяется следующим образом:
$$E=hν\ (3.1)$$
где $h$ — постоянная Планка, а $ν$ — частота света. За объяснение фотоэлектрического эффекта Эйнштейн получил Нобелевскую премию по физике в 1921 году.
Фотовольтаический эффект можно разделить на три основных процесса:
1. Генерация носителей заряда в результате поглощения фотонов в материалах, образующих соединение.
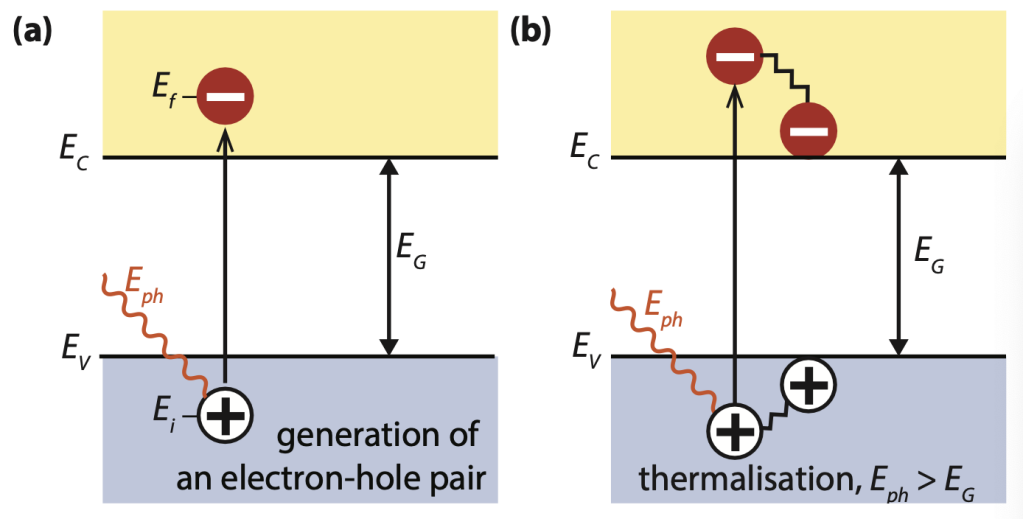
Поглощение фотона в материале означает, что его энергия используется для возбуждения электрона с начального энергетического уровня $E_{i}$ на более высокий энергетический уровень $E_{f}$, как показано на рис. 3.1 (a). Фотоны могут поглощаться только при наличии уровней энергии электронов $E_{i}$ и $E_{f}$, чтобы их разность равнялась энергии фотона, $hν=E_{f}-E_{i}$. В идеальном полупроводнике электроны могут занимать энергетические уровни ниже так называемого края валентной полосы, $E_{V}$, и выше так называемого края полосы проводимости, $E_{C}$. Между этими двумя полосами не существует разрешенных энергетических состояний, которые могли бы быть заселены электронами. Следовательно, эта разница энергий называется полосой пропускания, $E_{g}=E_{C}-E_{V}$. Если фотон с энергией меньше $E_{g}$ попадает в идеальный полупроводник, он не поглощается, а проходит через материал без взаимодействия.
В реальном полупроводнике полосы валентности и проводимости не плоские, а изменяются в зависимости от так называемого k-вектора, который описывает кристаллический момент полупроводника. Если максимум валентной полосы и минимум полосы проводимости приходятся на один и тот же k-вектор, электрон может быть возбужден из валентной полосы в полосу проводимости без изменения кристаллического момента. Такой полупроводник называется материалом с прямой полосой пропускания. Если электрон не может быть возбужден без изменения импульса кристалла, мы говорим о материале с непрямой полосой пропускания. Коэффициент поглощения в материале с прямой полосой пропускания гораздо выше, чем в материале с непрямой полосой пропускания, поэтому поглотитель может быть гораздо тоньше.
Если электрон возбуждается от $E_{i}$ до $E_{f}$, в точке $E_{i}$ образуется пустота. Эта пустота ведет себя как частица с положительным элементарным зарядом и называется дыркой. Поэтому поглощение фотона приводит к созданию электронно-дырочной пары, как показано на рис. 3.2. Излучаемая фотоном энергия преобразуется в химическую энергию электронно-дырочной пары. Максимальная эффективность преобразования радиационной энергии в химическую ограничена термодинамикой. Этот термодинамический предел лежит в диапазоне от 67 % для неконцентрированного солнечного света до 86 % для полностью концентрированного солнечного света.
Основы физики, необходимые для описания полупроводников, представлены далее.
2. Последующее разделение фотогенерированных носителей заряда в переходе.
Обычно электронно-дырочная пара рекомбинирует, то есть электрон возвращается на исходный энергетический уровень $E_{i}$, как показано на рис. 3.2. Затем энергия будет высвобождена либо в виде фотона (радиационная рекомбинация), либо передана другим электронам, дыркам или колебаниям решетки (нерадиационная рекомбинация). Если необходимо использовать энергию, запасенную в электронно-дырочной паре, для совершения работы во внешней цепи, по обе стороны поглотителя должны быть полупроницаемые мембраны, чтобы через одну мембрану могли выходить только электроны, а через другую — только дырки, как показано на рис. 3.2. В большинстве солнечных элементов эти мембраны образованы материалами n- и p-типа.
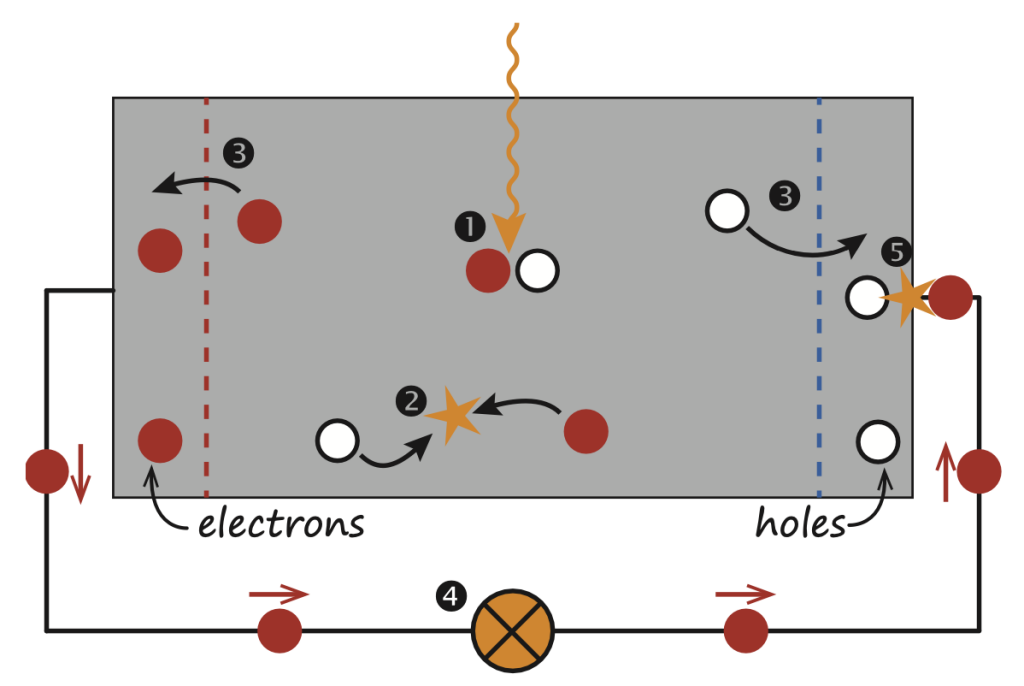
Солнечный элемент должен быть спроектирован таким образом, чтобы электроны и дырки могли достичь мембраны до того, как они рекомбинируют, т.е. время, необходимое носителям заряда для достижения мембраны, должно быть меньше времени их жизни. Это требование ограничивает толщину поглотителя. Мы подробно обсудим генерацию и рекомбинацию электронов и дырок далее.
3. Сбор фотогенерированных носителей заряда на клеммах перехода.
Наконец, носители заряда извлекаются из солнечных элементов с помощью электрических контактов, чтобы они могли совершить работу во внешней цепи (рис. 3.2). Химическая энергия электронно-дырочных пар преобразуется в электрическую энергию. После того как электроны прошли через цепь, они рекомбинируют с дырками на границе раздела металл-поглотитель, как показано на рис. 3.2.
Механизмы потерь
Два наиболее важных механизма потерь в солнечных элементах с одной зоной пропускания — это неспособность преобразовать фотоны с энергией ниже зоны пропускания в электричество и термализация фотонов с энергией, превышающей зону пропускания, как показано на рис. 3.1 (b). Только эти два механизма приводят к потере около половины солнечной энергии в процессе преобразования. Максимальная эффективность преобразования энергии однопереходного солнечного элемента значительно ниже термодинамического предела. Впервые этот предел для однопереходных солнечных элементов был рассчитан Шокли и Куиссером в 1961 году.
Подробный обзор механизмов потерь и обусловленных ими пределов эффективности рассматривается далее.
Добавить комментарий