Рубрика: Базовый курс

Наиболее общим пределом эффективности является термодинамический предел эффективности. В этом пределе фотоэлектрическое устройство рассматривается как термодинамический тепловой двигатель, как показано на рис. 10.1. Такой тепловой двигатель работает между двумя тепловыми резервуарами: горячим с температурой $T_{H}$  и холодным с температурой $T_{C}$. Для теплового двигателя важны три потока энергии. Во-первых, тепловой поток $\dot{Q}_{H}$ от горячего резервуара к двигателю. Во-вторых, работа $\dot{W}$, которую совершает двигатель, и, в-третьих, тепловой поток от двигателя к холодному резервуару, который служит теплоотводом, $\dot{Q}_{C}$.

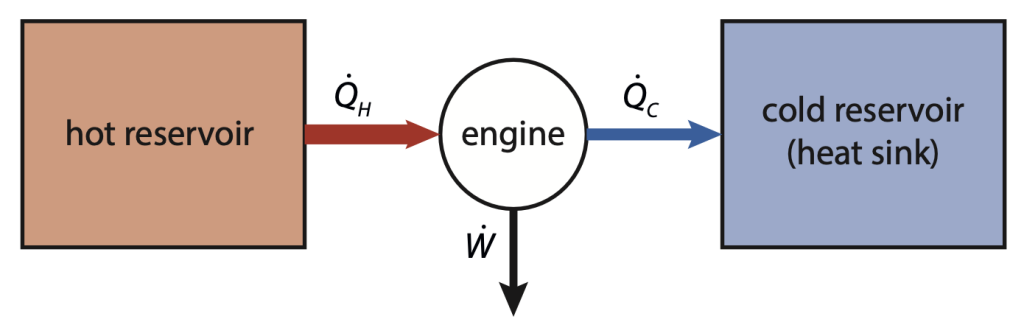
Очевидно, что третий поток энергии — это потери, и, следовательно, КПД теплового двигателя определяется следующим образом

$$\eta = \frac{\dot{W}}{\dot{Q}_{H}}\ (10.1)$$

Второй закон термодинамики учит нас, что энтропия изолированной системы никогда не уменьшается. Она только увеличивается или остается неизменной. В то время как тепловые потоки $\dot{Q}_{H}$ и $\dot{Q}_{C}$ несут в себе энтропию, совершенная работа $\dot{W}$ представляет собой форму энергии, свободную от энтропии. Термодинамика учит нас, что существует предел эффективности преобразования тепла в энергию, свободную от энтропии. (Идеальный) двигатель, имеющий этот максимальный КПД, называется двигателем Карно, и его КПД определяется следующим образом

$${\eta}_{\text{Carnot}}=1-\frac{T_{C}}{T_{H}}\ (10.2)$$

Для двигателя Карно энтропия не увеличивается. Обратите внимание, что все температуры должны быть даны в температурной шкале, где абсолютный ноль принимает значение 0. Например, такой шкалой является шкала Кельвина. Из уравнения (10.2) уже видны две важные тенденции, которые в принципе справедливы для любого теплового двигателя, т. е. и для паровых машин, и для двигателей внутреннего сгорания. КПД увеличивается, если более высокая температура  $T_{H}$ повышается и/или более низкая температура $T_{C}$ понижается.

Давайте теперь рассмотрим солнечный элемент, который мы представляем как тепловой двигатель, работающий между поглотителем температуры $T_{A}$ (это наш горячий резервуар) и холодным резервуаром, который задается окружающей средой и который мы предполагаем имеющим температуру $T_{C}=300\text{K}$. Что этот тепловой двигатель фактически делает, так это преобразует энергию, запасенную в тепле поглотителя, в химическую энергию без энтропии, которая хранится в парах электрон-дырка. Здесь мы можем предположить, что преобразование химической энергии в электрическую происходит без потерь, т.е. с КПД, равным 1. Очевидно, что КПД этого термодинамического теплового двигателя определяется следующим образом

$${\eta}_{TD}=1-\frac{T_{C}}{T_{A}}\ (10.3)$$

Поглотитель будет нагреваться, поглощая солнечный свет. Рассматривая идеальную ситуацию, мы предполагаем, что поглотитель — это черное тело, которое поглощает все падающее излучение. Далее, мы предполагаем, что солнце — это черное тело с температурой $T_{S}=6000\text{K}$. Как мы видели ранее, солнечное излучение, падающее на поглотитель, определяется следующим образом

$$I_{e}^{S}={\sigma}T_{S}^{4}{\Omega}_{\text{inc}}\ (10.4)$$

где ${\Omega}_{\text{inc}}$ — телесный угол, охватываемый падающим солнечным светом. Поскольку поглотитель является черным телом с температурой $T_{A}$, он также будет испускать излучение. Светимость поглотителя определяется следующим образом

$$E_{e}^{A}={\sigma}T_{A}^{4}{\Omega}_{\text{emit}}\ (10.5)$$

${\Omega}_{\text{emit}}$ — телесный угол, в который поглотитель может излучать.

Легко видеть, что эффективность процесса поглощения определяется следующим образом

$${\eta}_{A}=\frac{I_{e}^{S}-E_{e}^{A}}{I_{e}^{S}}=1-\frac{E_{e}^{A}}{I_{e}^{S}}=1-\frac{{\Omega}_{\text{emit}}T_{A}^{4}}{{\Omega}_{\text{inc}}T_{S}^{4}}\ (10.6)$$

Эффективность абсорбера можно повысить за счет увеличения ${\Omega}_{\text{inc}}$, что может быть достигнуто путем концентрации солнечного света. При максимальной концентрации солнечный свет будет попадать на абсорбер со всех углов полусферы, т. е. ${\Omega}_{\text{inc}}^{\text{max}}=2\pi$. Мы предполагаем, что абсорбер с верхней стороны открыт для окружающей среды и, следовательно, для солнца. Его нижняя сторона соединена с тепловым двигателем, поэтому радиационные потери могут происходить только через верхнюю сторону. Поэтому также ${\Omega}_{\text{emit}}=2\pi$. Таким образом, максимальная эффективность абсорбера достигается при максимальной концентрации и определяется следующим образом

$${\eta}_{A}^{\text{max}}=1-\frac{T_{A}^{4}}{T_{S}^{4}}\ (10.7)$$

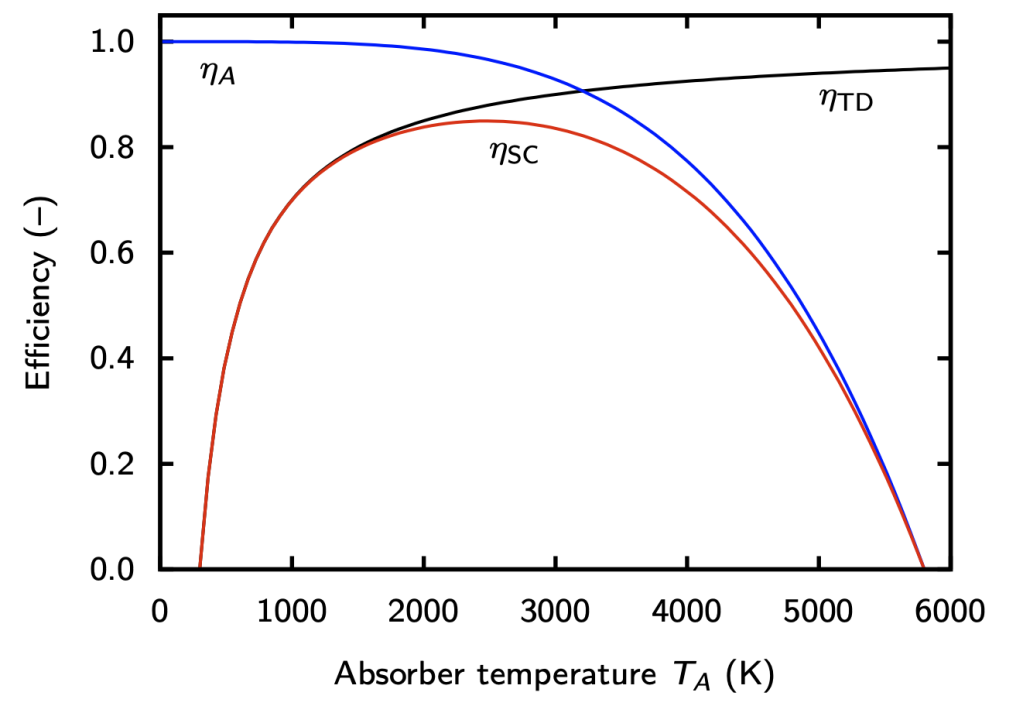
Заметим, что ${\eta}_{A}$ тем больше, чем меньше $T_{A}$, а эффективность теплового двигателя ${\eta}_{TD}$ тем больше, чем выше $T_{A}$.

Для полного КПД идеального солнечного элемента объединим уравнение (10.3) с уравнением (10.7) и получим

$${\eta}_{SC}=(1-\frac{T_{A}^{4}}{T_{S}^{4}})(1-\frac{T_{C}}{T_{A}})\ (10.8)$$

На рис. 10.2 показаны эффективность абсорбера, термодинамическая эффективность и эффективность солнечного элемента. Мы видим, что КПД солнечного элемента достигает максимума около 85% при температуре абсорбера 2480 К. Обратите внимание, что модель солнечного элемента, представленная в этом разделе, не похожа на реальный солнечный элемент, а предназначена только для обсуждения физического предела преобразования солнечного излучения в электричество. Было проведено несколько гораздо более детальных исследований термодинамического предела.

В этой публикации мы представим очень простую модель солнечного элемента. Многие понятия, представленные в этой главе, будут новыми, но, тем не менее, основные принципы работы солнечной батареи должны быть понятны. Все аспекты, представленные здесь, будут более подробно рассмотрены далее.

Принцип работы солнечных батарей основан на фотовольтаическом эффекте, т.е. возникновении разности потенциалов на стыке двух различных материалов в ответ на электромагнитное излучение. Фотовольтаический эффект тесно связан с фотоэлектрическим эффектом, когда электроны испускаются из материала, поглотившего свет с частотой выше пороговой частоты, зависящей от материала. В 1905 году Альберт Эйнштейн понял, что этот эффект можно объяснить, если предположить, что свет состоит из четко определенных квантов энергии, называемых фотонами. Энергия такого фотона определяется следующим образом:

$$E=hν\ (3.1)$$

где $h$ — постоянная Планка, а $ν$ — частота света. За объяснение фотоэлектрического эффекта Эйнштейн получил Нобелевскую премию по физике в 1921 году.

Фотовольтаический эффект можно разделить на три основных процесса:

1. Генерация носителей заряда в результате поглощения фотонов в материалах, образующих соединение.

Поглощение фотона в материале означает, что его энергия используется для возбуждения электрона с начального энергетического уровня $E_{i}$ на более высокий энергетический уровень $E_{f}$, как показано на рис. 3.1 (a). Фотоны могут поглощаться только при наличии уровней энергии электронов $E_{i}$ и $E_{f}$, чтобы их разность равнялась энергии фотона, $hν=E_{f}-E_{i}$. В идеальном полупроводнике электроны могут занимать энергетические уровни ниже так называемого края валентной полосы, $E_{V}$, и выше так называемого края полосы проводимости, $E_{C}$. Между этими двумя полосами не существует разрешенных энергетических состояний, которые могли бы быть заселены электронами. Следовательно, эта разница энергий называется полосой пропускания, $E_{g}=E_{C}-E_{V}$. Если фотон с энергией меньше $E_{g}$ попадает в идеальный полупроводник, он не поглощается, а проходит через материал без взаимодействия.

В реальном полупроводнике полосы валентности и проводимости не плоские, а изменяются в зависимости от так называемого k-вектора, который описывает кристаллический момент полупроводника. Если максимум валентной полосы и минимум полосы проводимости приходятся на один и тот же k-вектор, электрон может быть возбужден из валентной полосы в полосу проводимости без изменения кристаллического момента. Такой полупроводник называется материалом с прямой полосой пропускания. Если электрон не может быть возбужден без изменения импульса кристалла, мы говорим о материале с непрямой полосой пропускания. Коэффициент поглощения в материале с прямой полосой пропускания гораздо выше, чем в материале с непрямой полосой пропускания, поэтому поглотитель может быть гораздо тоньше.

Если электрон возбуждается от $E_{i}$ до $E_{f}$, в точке $E_{i}$ образуется пустота. Эта пустота ведет себя как частица с положительным элементарным зарядом и называется дыркой. Поэтому поглощение фотона приводит к созданию электронно-дырочной пары, как показано на рис. 3.2. Излучаемая фотоном энергия преобразуется в химическую энергию электронно-дырочной пары. Максимальная эффективность преобразования радиационной энергии в химическую ограничена термодинамикой. Этот термодинамический предел лежит в диапазоне от 67 % для неконцентрированного солнечного света до 86 % для полностью концентрированного солнечного света.

Основы физики, необходимые для описания полупроводников, представлены далее.

2. Последующее разделение фотогенерированных носителей заряда в переходе.

Обычно электронно-дырочная пара рекомбинирует, то есть электрон возвращается на исходный энергетический уровень $E_{i}$, как показано на рис. 3.2. Затем энергия будет высвобождена либо в виде фотона (радиационная рекомбинация), либо передана другим электронам, дыркам или колебаниям решетки (нерадиационная рекомбинация). Если необходимо использовать энергию, запасенную в электронно-дырочной паре, для совершения работы во внешней цепи, по обе стороны поглотителя должны быть полупроницаемые мембраны, чтобы через одну мембрану могли выходить только электроны, а через другую — только дырки, как показано на рис. 3.2. В большинстве солнечных элементов эти мембраны образованы материалами n- и p-типа.

Солнечный элемент должен быть спроектирован таким образом, чтобы электроны и дырки могли достичь мембраны до того, как они рекомбинируют, т.е. время, необходимое носителям заряда для достижения мембраны, должно быть меньше времени их жизни. Это требование ограничивает толщину поглотителя. Мы подробно обсудим генерацию и рекомбинацию электронов и дырок далее.

3. Сбор фотогенерированных носителей заряда на клеммах перехода.

Наконец, носители заряда извлекаются из солнечных элементов с помощью электрических контактов, чтобы они могли совершить работу во внешней цепи (рис. 3.2). Химическая энергия электронно-дырочных пар преобразуется в электрическую энергию. После того как электроны прошли через цепь, они рекомбинируют с дырками на границе раздела металл-поглотитель, как показано на рис. 3.2.

Механизмы потерь

Два наиболее важных механизма потерь в солнечных элементах с одной зоной пропускания — это неспособность преобразовать фотоны с энергией ниже зоны пропускания в электричество и термализация фотонов с энергией, превышающей зону пропускания, как показано на рис. 3.1 (b). Только эти два механизма приводят к потере около половины солнечной энергии в процессе преобразования. Максимальная эффективность преобразования энергии однопереходного солнечного элемента значительно ниже термодинамического предела. Впервые этот предел для однопереходных солнечных элементов был рассчитан Шокли и Куиссером в 1961 году.

Подробный обзор механизмов потерь и обусловленных ими пределов эффективности рассматривается далее.